Answer:
$51134
Step-by-step explanation:
First, we need to find the area of the land. So, we need to identify the height of the triangle h as:
Then, using the trigonometric functions, we can calculate the value of h as:
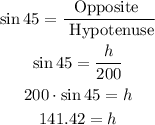
Now, the area of the triangle in square yards is:
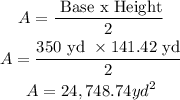
1 acre is equal to 1840 square yards, so the area in acres is:
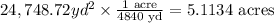
Finally, the price of the land can be calculated as:
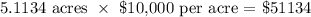
Therefore, the land cost $51134