Given:
• Mass of car, m = 1600 kg
,
• Force, N = 8000 N
,
• Angle, θ = 30 degrees
Let's find the car's new acceleration on this angle ignoring the force due to air resistance.
First apply the formula which shows the weight of the car that is parallel to this parallel to this angle:
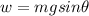
Where:
m - 1600 kg
g is acceleration due to gravity = 9.8 m/s²
θ = 30 degrees
Plug in values and solve for w:
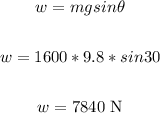
Now, the weight of the car parallel to the angle is 7840 N.
To find the acceleration, apply Newton's Second Law of motion:
ΣF = ma
F = ma + w
Where a is the acceleration.
Rewrite the formula for a and solve:
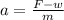
Plug in values and solve for a:
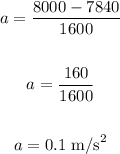
Therefore, the new acceleration of the car is 0.1 m/s².
ANSWER:
0.1