Recall that for a, b, and c to be the lengths of a triangle they must satisfy the following inequalities:
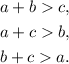
Therefore, if we call the other side x, it must satisfy that:
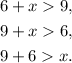
Solving each inequality for x, we get:
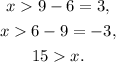
Therefore, x must be greater than 3 inches but less than 15 inches.
Answer: The possible lengths of the third side must be greater than 3 inches but less than 15 inches