1 Answer

Kevin Rave · Answer 1 · 2023-02-25T12:16:07+0000

Recall that the sum of the interior angles of a convex polygon with n sides is:

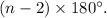
$(n-2)*180^(\circ).$

Therefore:

12) If the sum of the interior angles of a convex polygon is 3240 degrees, then we can set the following equation:

$(n-2)*180^{}=3240.$

Dividing the above equation by 180 we get:

$\begin{gathered} ((n-2)*180)/(180)=(3240)/(180), \\ n-2=18. \end{gathered}$

Adding 2 to the above equation we get:

$\begin{gathered} n-2+2=18+2, \\ n=20. \end{gathered}$

13) If the sum of the interior angles of a convex polygon is 6660 degrees, then we can set the following equation:

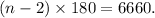
Dividing the above equation by 180 we get:

$\begin{gathered} ((n-2)*180)/(180)=(6660)/(180), \\ n-2=37. \end{gathered}$

Adding 2 to the above equation we get:

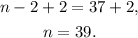
$\begin{gathered} n-2+2=37+2, \\ n=39. \end{gathered}$

Answer:

12) 20.

13) 39.

Please log in or register to add a comment.