Given the logarithmic equation:
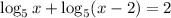
Let's solve for the two potential roots, A and B, where A ≤ B.
Apply the rules of loagarithm:
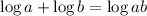
Thus, we have:
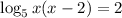
Solving further:

Subtract 25 from both sides of the equation:
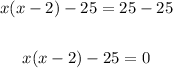
Expand using distributive property:
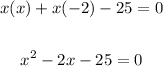
Now solve using the quadratic formula:
![\frac{-b\pm\sqrt[]{b^2-4ac}}{2b}](https://img.qammunity.org/2023/formulas/mathematics/college/n0osarea32g3mux4bg5kimv52vbbd6ybn7.png)
To find the values of a, b, and c, apply the general quadratic equation:
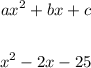
Where:
a = 1
b = -2
c = -25
Thus, we have:
![\begin{gathered} \frac{-(-2)\pm\sqrt[]{-2^2-4(1)(-25)}}{2(1)} \\ \\ x=\frac{2\pm\sqrt[]{4+100}}{2} \\ \\ x=\frac{2\pm\sqrt[]{104}}{2} \\ \\ x=\frac{2\pm\sqrt[]{26\ast4}}{2} \\ \\ x=\frac{2\pm2\sqrt[]{26}}{2} \\ \\ x=(2)/(2)\pm\frac{2\sqrt[]{26}}{2} \\ \\ x=1\pm\sqrt[]{26} \\ \\ x=1-\sqrt[]{26},\text{ 1+}\sqrt[]{26} \\ \\ x=-4.1,6.1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yw7xd7dh7sl3xvgt0mowkhwca8phmwls5f.png)
Hence, we have the values of A and B:
A = -4.099
B = 6.099
A and B are actually roots.
ANSWER:
A = -4.1
B = 6.1
Yes, A is actually a root
Yes, B is actually a root.