Question

The data set below shows the temperature, in degrees Fahrenheit, of a mug of tea compared tothe time in minutes after being poured out of the tea kettle. An exponential regression wasperformed on this data to obtain the model y - 174.4(0.987)*. Create a residual plot andexplain why the model is or is not good fit for this data.

Answer 1

Given the model of the Exponential Regression:

`y=174.4(0.987)^x`

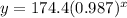
By definition:

`Residual=Observed\text{ }y\text{ }value-Predicted\text{ }y\text{ }value`

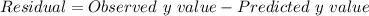
You can see in the table the observed y-values (the temperature in Fahrenheit)

In order to find the Predicted y-values, you need to substitute all the x-values given in the table (the time in minutes) into the equation and then evaluate. You get:

`y=174.4(0.987)^5\approx163.35`
`y=174.4(0.987)^8\approx157.07`
`y=174.4(0.987)^(11)\approx151.02`
`y=174.4(0.987)^(15)\approx143.32`
`y=174.4(0.987)^(18)\approx137.80`
`y=174.4(0.987)^(22)\approx130.77`
`y=174.4(0.987)^(25)\approx125.74`
`y=174.4(0.987)^(29)\approx119.33`
`y=174.4(0.987)^(32)\approx114.73`
`y=174.4(0.987)^(35)\approx110.32`

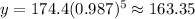
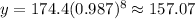
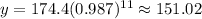
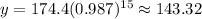
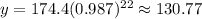
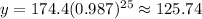
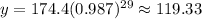
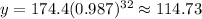
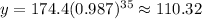
Now you have these points:

Therefore, you can plot them on the Coordinate Plane:

By definition, when the residual plot shows a pattern, a non-linear regression model is appropriate for the data. Therefore, the Exponential Regression Model is a good fit.

Hence, the answer is:

- Residual Plot:

- First option.