Answer:
9 years
Step-by-step explanation:
One thing is for sure: since Mars is farther away from the sun, one martian year is greater than one Earth year. This, in turn, means that if our student lived on Mars and counted her age in terms of martian years, then she would certainly be less than 17 years old in martian years.
Now, Kepler's third law relates the orbital period ( what we call a year) to the distance from the sun.
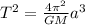
where
T = oribtal period
G = gravitational constant
M = mass of the sun
a = distance from the sun.
Now, in the case of the earth, we have

where
T_E = earth's orbital period
a_E = earth's distance from the sun.
Now, in the case of mars, we know that
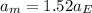
therefore, for mars, Kepler's third law gives
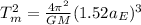
which we can rewrite to get
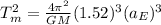
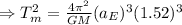
Now at this point remember that

therefore, we have
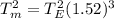
Taking the square root of both sides gives
![T_m=\sqrt[]{T^2_E(1.52)^3}](https://img.qammunity.org/2023/formulas/physics/college/q93vrz81fdkdplzptmm8mn303hj4zmd6xu.png)
![T_m=\sqrt[]{(1.52)^3}T^{}_E](https://img.qammunity.org/2023/formulas/physics/college/f0cqguk52qkrdiwab1wnq1miatcwq8mrue.png)
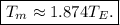
This tells us that one martian year is about 1.874 earth years.
Or equivalently one earth year is about 1/1.874 martian years.
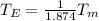
Therefore, if a student is 17 years old on Earth, then er equivalent age on mars would be:
![undefined]()