Question

Find the solutions of the following trigonometric equation in the interval [0,2π). tan^2x+secx=1

Answer 1

`\tan ^2x+\sec x=1`

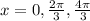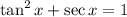
Given the next trigonometric identity:

`\begin{gathered} \tan ^2x+1=\sec ^2x \\ \text{ Or} \\ \tan ^2x=\sec ^2x-1 \end{gathered}`

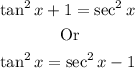
Substituting this identity into the equation:

`\sec ^2x-1+\sec x=1`

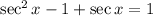
Subtracting 1 at both sides of the equation:

`\begin{gathered} \sec ^2x-1+\sec x-1=1-1 \\ \sec ^2x+\sec x-2=0 \end{gathered}`

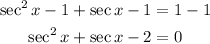
Replacing with:

`\begin{gathered} y=\sec x \\ y^2=\sec ^2x \end{gathered}`

we get:

`y^2+y-2=0`

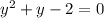
Applying the quadratic formula with a = 1, b = 1 and c = -2:

`\begin{gathered} y_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y_(1,2)=\frac{-1\pm\sqrt[]{1^2-4\cdot1\cdot(-2)}}{2\cdot1} \\ y_(1,2)=\frac{-1\pm\sqrt[]{9}}{2} \\ y_1=(-1+3)/(2)=1 \\ y_2=(-1-3)/(2)=-2 \end{gathered}`

Recalling that y = sec(x), then we have two options:

`\begin{gathered} \sec x=1 \\ \text{and} \\ \sec x=-2 \end{gathered}`

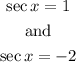
By definition:

`\sec x=(1)/(\cos x)`

Therefore, the first option is:

`\begin{gathered} (1)/(\cos x)=1 \\ ((1)/(\cos x))^(-1)=1^(-1) \\ \cos x=1 \end{gathered}`

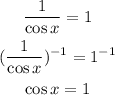
In the interval of x [0,2π), the solution to this equation is 0.

Now, considering the second option:

`\begin{gathered} (1)/(\cos x)=-2 \\ ((1)/(\cos x))^(-1)=(-2)^(-1) \\ \cos x=-(1)/(2) \end{gathered}`

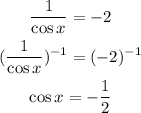
In the interval of x [0,2π), the solutions to this equation are 2π/3 and 4π/3.

In summary, the solutions to tan^2⁡(x) + sec(x) = 1 are:

`x=0,(2\pi)/(3),(4\pi)/(3)`