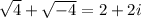Complex numbers are numbers in the form
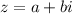
where i represents the imaginary number defined as the square root of minus one.
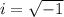
We call a as the real part of the complex number and b the imaginary part.
We want to rewrite the number
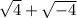
in terms of the imaginary constant.
Using the following property
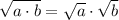
We can rewrite the second term of our sum as
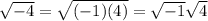
Then, our number can be rewritten as
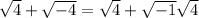
Using the definition of the imaginary unit we can rewrite our number as
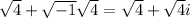
Then, we can rewrite the square roots as
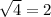
The simplified version of our number is