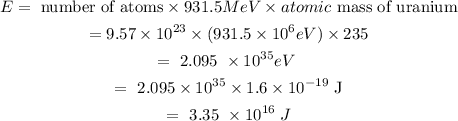Given that the mass of uranium is m = 0.375 kg = 375 g.
We have to find the energy.
First, we need to find the number of moles.
The number of moles can be calculated as
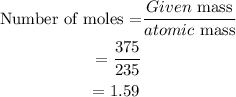
Next, we have to convert the number of moles into the number of atoms.
The number of atoms will be
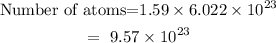
One atomic mass unit releases 931.5 MeV energy.
The energy can be calculated as