To find the distance across the lake, first consider that triangles ADE and ABC are congruent. Then, you have the relation between the following proportions of the two triangles:
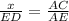
where:
AC = AE + EC = 25 ft + 30 ft = 55 ft
ED = 15 ft
AE = 25 ft
solve the equation for x and replace the values of the segments:

x represents the distance across the lake.
Hence, the distance is 33 ft