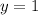Question

Analyze and sketch a graph of the function. Find any intercepts, relative extrema, points of inflection, and asymptotes. (If an answer does not exist, enter DNE.)

Answer 1

Given the function;

`y=(x^2)/(x^2+48)`

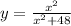
The graph of the function is;

The x-intercept is;

`(0,0)`

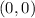
The y-intercept is;

`(0,0)`

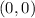
The relative minimum is;

`(0,0)`

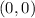
The relative maximum does not exist. Thus;

`DNE=`

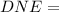
The points of inflection are;

`\begin{gathered} (-4,(1)/(4))\ldots\ldots..\ldots.smaller\text{ x-value} \\ (4,(1)/(4))\ldots.\ldots\ldots\ldots\text{.larger x-value} \end{gathered}`

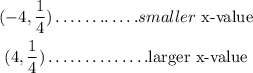
Lastly, it has no vertical asymptote. The equation of the asymptote is;

`y=1`