Question

If 320 J of work is done on a spring with a spring constant of 730 N/m, how far will it stretch?1) 0.58 m2) 0.87 m3) 0.61 m4) 0.94 m

Answer 1

Given,

The work done on the spring, U=320 J

The spring constant, k=730 N/m

The work done on the spring is stored in it as the spring potential energy. And it is given by

`U=(1)/(2)kx^2`

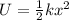
On rearranging the above equation,

`\begin{gathered} x^2=(2U)/(k) \\ \Rightarrow x=\sqrt[]{(2U)/(k)} \end{gathered}`

On substituting the known values in the above equation,

`\begin{gathered} x=\sqrt[]{(2*320)/(730)} \\ =0.94\text{ m} \end{gathered}`

Thus the spring stretches for 0.94 m. Therefore the correct answer is option 4.