Question

What is the equation of the line that passes through the point (2,-2) and has aslope of -1/2

Answer 1

Concept

Use slope and a point form to find the equation of the line.

Method

Given data

slope = -1/2

Given point = (2,-2)

Next, write the equation of a slope-point form to find the equation of a line.

`\begin{gathered} \text{Slope}-po\text{int equation of a line} \\ m\text{ = }(y-y_1)/(x-x_1) \end{gathered}`

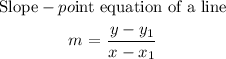
Next, label the given data

m = -1/2

x1 = 2 and y1 = -2

Substituting m, x1 and y1 into the equation we get

`\begin{gathered} m=(y-y_1)/(x-x_1) \\ (-1)/(2)\text{ = }\frac{y\text{ -(-2)}}{x\text{ - 2}} \\ (-1)/(2)\text{ = }\frac{y\text{ + 2}}{x\text{ -2}} \end{gathered}`

Cross multiply

`\begin{gathered} 2(\text{ y + 2 ) = -1 ( x - 2 )} \\ 2y\text{ + 4 = -x + 2} \\ \text{collect like terms} \\ 2y\text{ = -x + 2 - 4} \\ 2y\text{ = -x - }2 \\ \text{Divide through by 2} \\ (2y)/(2)\text{ = }(-1)/(2)x\text{ - }(2)/(2) \\ y\text{ = }(-1)/(2)x\text{ - }1 \end{gathered}`

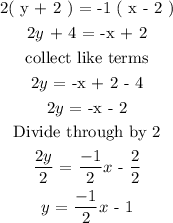
Final answer

`\text{Equation of a line is: y = }(-1)/(2)x\text{ - 1}`