Question

You have a cup with 17 coins inside. The total inside the cup is $5.50. Determine how many half dollars and quarters are inside the cup.

Answer 1

Let x be the number of half dollar and y, the number of quarter dollar

Thus,

`x+y=17\text{ -----eq i)}`

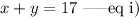
Half dollar is 50cent, quarter dollar is 25cents,

Thus,

`0.5x+0.25y=5.50\text{ -----eq i}i)`

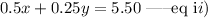
Solving the two(2) equations simultaneously; we have:

From eq i)

`\begin{gathered} x+y=17 \\ x=17-y\text{ -----eq }iii) \end{gathered}`

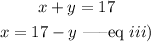
Put eq iii) into ii), we have:

`\begin{gathered} 0.5x+0.25y=5.50 \\ 0.5(17-y)+0.25y=5.50 \\ 8.5-0.5y+0.25y=5.50 \\ 8.5-0.25y=5.50 \\ 8.5-5.50=0.25y \\ 0.25y=3 \\ y=(3)/(0.25) \\ y=12 \end{gathered}`

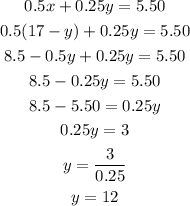
From eq iii)

`\begin{gathered} x=17-y \\ x=17-12 \\ x=5 \end{gathered}`

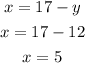
Hence, there are 5 half dollars and 12 quarter dollars inside the cup