Given:
Base distance = 20 ft.
Angle = 50
Ground height = 5 ft
Find-:
The height of the tree
Explanation-:
The height of the tree
The height of the tree is:
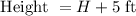
Value of H is:
In triangle ABC

Trignometry formula is:
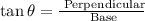
The value of "H" is:

So the height of the tree is:

Height of the tree is 29 feet.