Question

All 13 of the orangutans at a certain zoo contract a very serious disease which claims 75% of its victims (if an orangutan contracts the disease, the probability that it will die is 0.75). What is the probability, rounded to four decimal places, that exactly 2 of the orangutans at this zoo will survive?Type your answer here

Answer 1

In order to calculate the probability, we can use the formula below:

`P\left(x\right)=\lparen n\text{ }x)*p^x*\left(1-p\right)^(n-x)`

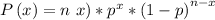
Where n is the total number of elements, x is the desired amount and p is the probability of the desired event happening.

So, if exactly 2 orangutans will survive, that means 11 will die, so let's use n = 13, x = 11 and p = 0.75.

Also, the expression (n x) means the binomial of n and x:

`\left(n\text{ x}\right)=(n!)/(x!\left(n-x\right)!)`

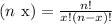
So we have:

`\begin{gathered} P\left(x=11\right)=\left(13\text{ 11}\right)*0.75^(11)*0.25^2 \\ P\left(x=11\right)=(13!)/(11!2!)*0.042235*0.0625 \\ P\left(x=11\right)=(13*12)/(2)*0.042235*0.0625 \\ P\left(x=11\right)=0.2059 \end{gathered}`

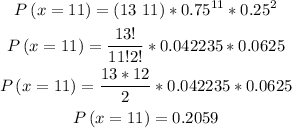
Therefore the probability is 0.2059.