Given:
The charge of X is

The charge of Y is

The distance between the charges is r = 80 cm.
To find whether there is an increase or decrease in the force of attraction/repulsion if the new charge of y is
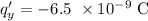
and the distance between the charges is the same.
Step-by-step explanation:
The charges q_x and q_y will have the force of attraction as they have opposite charges.
The magnitude of the force is given by the formula

Here, the k is the electrostatic constant.
The distance between the charges is the same and the charge on X is also the same.
Thus, the force
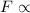
The new charge has a magnitude more than the old charge on Y.
Thus, the force of attraction will increase due to the increase in the magnitude of the charge.
Final Answer: The electrical force of attraction will increase.