Given:
The width of the rectangle is 9 yd.
Required:
To find the area of the shaded region.
Step-by-step explanation:
From the given figure,
Width of the rectangle is 9 yd.
Therefore, the radius of the semicircle is 9yd.
And the length of the rectangle is diameter of the semicircle.
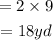
Now, the area of the rectangle is,
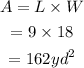
Now the area of the semicircle is,

Now the area of the shaded region = Area of the rectangle - Area of the semicircle.
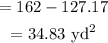
Final Answer:
The area of the shaded region is 34.83 yd square.