Question

Given that DE¯¯¯¯¯¯¯¯, DF¯¯¯¯¯¯¯¯, and EF¯¯¯¯¯¯¯¯ are midsegments of △ABC, and DE=3.2 feet, EF=4 feet, and DF=2.4 feet, what is the perimeter of △AB

Answer 1

Given: The triangle ABC is provided with DE = 3.2 feet, EF = 4 feet and DF = 2.4 feet.

To find: The perimeter of the triangle ABC.

Step-by-step explanation:

The triangle ABC is given where DE , EF and DF are the midsegments of the triangle ABC.

If DE is the midsegment then using midsegment theorem we have

`\begin{gathered} DE=(1)/(2)BC \\ BC=2DE \\ BC=2*3.2 \\ BC=6.4 \\ \end{gathered}`

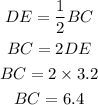
Since, EF is the midsegment then using midsegment theorem we have

`\begin{gathered} EF=(1)/(2)AB \\ AB=2EF \\ AB=2*4 \\ AB=8 \end{gathered}`

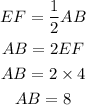
Since, DF is the midsegment then using midsegment theorem we have

`\begin{gathered} DF=(1)/(2)AC \\ AC=2DF \\ AC=2*2.4 \\ AC=4.8 \end{gathered}`

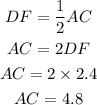
We have the sides of the triangle as AB = 8 feet, BC = 6.4 feet and AC = 4.8 feet.

The perimeter of the triangle ABC will be :

P = AB+BC+AC

=8+6.4+4.8

=19.2

Therefore, the perimeter of the triangle is P = 19.2 feet

Final Answer: The perimeter is P = 19.2 feet.