In order to solve this question, we need to use the z-score z of value x, belonging to a normal distribution with mean μ and standard deviation σ.
z is defined as:

In this problem, we have, in pounds:
μ = 8.9
σ = 1.1
PART 1
So, the percentage of domestic house cats that weigh less than 7.8 pounds is:
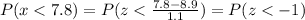
And from a z-score table, we have:
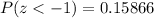
Therefore, the percentage of domestic house cats that weigh less than 7.8 pounds is approximately 0.1587 or 15.87%.
PART 2
The percentage of domestic house cats that weigh more than 11.1 pounds is 1 minus the percentage of them that weigh less than that:
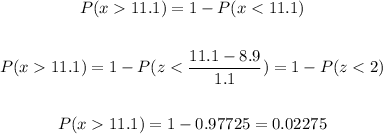
Therefore, the percentage of domestic house cats that weigh more than 11.1 pounds is approximately 0.0228 or 2.28%.
PART 3
The domestic house cat weighing 9 pounds is in percentile P(x<9):
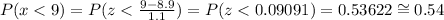
Therefore, a domestic house cat weighing 9 pounds is in the 54th percentile.