Question

Help me out with this question

Answer 1

We have to calculate the probability of having at least 7 defects in a 26 sq ft metal sheet.

The number of defects is modeled by a Poisson distribution with an average umber of defects of 4 defects per 16 sq ft.

We can write the parameter rate as:

Then, we have to calculate the probability of having at least 7 defects in a 26 sq ft metal sheet.

The probability can be calculated as:

`P(k\ge7)=1-P(k<7)=1-\sum ^6_(k=0)P(k)`

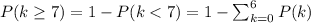
The parameter, average number of defects, for this metal sheet can be calculated as:

Then, we can calculate all the probabilities from k=0 to k=6 as:

`\begin{gathered} P(0)=6.5^0\cdot e^(-6.5)/0!=1*0.0015/1=0.002 \\ P(1)=6.5^1\cdot e^(-6.5)/1!=6.5*0.0015/1=0.01 \\ P(2)=6.5^2\cdot e^(-6.5)/2!=42.25*0.0015/2=0.032 \\ P(3)=6.5^3\cdot e^(-6.5)/3!=274.625*0.0015/6=0.069 \\ P(4)=6.5^4\cdot e^(-6.5)/4!=1785.0625*0.0015/24=0.112 \\ P(5)=6.5^5\cdot e^(-6.5)/5!=11602.9063*0.0015/120=0.145 \\ P(6)=6.5^6\cdot e^(-6.5)/6!=75418.8906*0.0015/720=0.157 \end{gathered}`

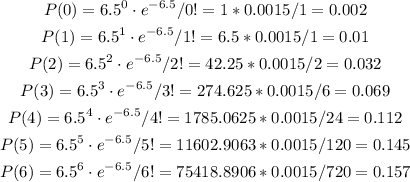
Then, we can calculate:

`\begin{gathered} P(x\ge7)=1-P(x<7) \\ P(x\ge7)=1-(0.002+0.01+0.032+0.069+0.112+0.145+0.157) \\ P(x\ge7)=1-0.525 \\ P(x\ge7)=0.475 \end{gathered}`

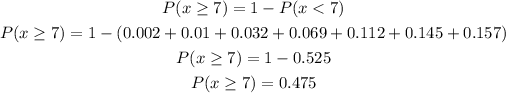
The probability of having 7 or more defects in the 26 sq ft metal sheet is 0.475.