Answer:
P(2426 < X < 2861) =0.9079
Explanation:
• The average life of the bulb = 2710 hours
,
• The standard deviation = 111 hours
We want to find the probability that a particular bulb will last from 2426 to 2861 hours.
Using the z-score formula below:
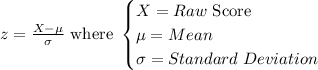
We standardize each of the given values:
[tex]\begin{gathered} P\left(2426From the z-score table:[tex]P(-2.56
The probability that a particular bulb will last from 2426 to 2861 hours is 0.9079.