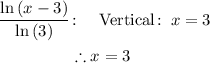Let's begin by listing out the given information:
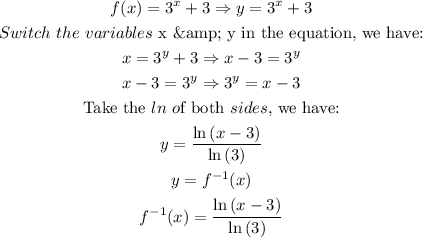
2.
The domain of a function is the set of input or argument values for which the function is real and defined. This is given by:
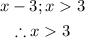
3.
The range of a function is the set of output values for which the function is defined. This is given by:
![\begin{gathered} 3^x+3\colon-\infty\: <strong>4. </strong><p>The range of f(x) is the domain of f^-1(x) since they are inverse of one another. </p>[tex]\begin{gathered} f\mleft(x\mright)=3^x+3 \\ x=0 \\ f(0)=3^0+3=1+3=4 \\ x=1 \\ f(1)=3^1+3=3+3=6 \\ x=2 \\ f(2)=3^2+3=9+3=12 \\ \end{gathered}]()
Therefore, the domain of f^-1(x) increases
5.
The asymptote of a curve is a line such that the distance between the curve and the line approaches zero