Question

Here is a sample data set.241.1413.2413.2408.4343.6412.2353432.7457.9437.7399.1358.1435.2426.3413.2299.2382.5344.9427.3384.2438.3315.2458357.1337.2402.6396.6400.4343.6394.4303.5441.9316.7239.2410.1343.6404.8405.7437.9394.4461.9385.6378.5373.3286.8311.7274.9371.9379.1436.4254.7402.3407.5322.3Find the first quartile for this data set.Q.Find the third quartile for this data set.Q =Find the interquartile range for this data set.IQR =

Answer 1

We are asked to find the 1st and 3rd quartiles and the interquartile range for the given data.

Let us first arrange the data in ascending order (least to greatest)

239.2

241.1

254.7

274.9

286.8

299.2

303.5

311.7

315.2

316.7

322.3

337.2

343.6

343.6

343.6

344.9

353

357.1

358.1

371.9

373.3

378.5

379.1

382.5

384.2

385.6

394.4

394.4

396.6

399.1

400.4

402.3

402.6

404.8

405.7

407.5

408.4

410.1

412.2

413.2

413.2

413.2

426.3

427.3

432.7

435.2

436.4

437.7

437.9

438.3

441.9

457.9

458

461.9

The position of the 1st quartile is given by

`Q_1=(1)/(4)\cdot(n+1)^(th)`

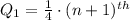
Where n is the total number of data values (n = 54)

`Q_1=(1)/(4)(54+1)=13.5^(th)`

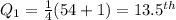
The 1st quartile is between the 13th and 14th value.

13th value = 343.6

14th value = 343.6

Take the average of these two values

`Q_1=(343.6+343.6)/(2)=343.6`

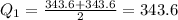
The 1st quartile is 343.6

The position of the 3rd quartile is given by

`\begin{gathered} Q_3=(3)/(4)(n+1)^(th) \\ Q_3=(3)/(4)(54+1)=41.25^(th) \end{gathered}`

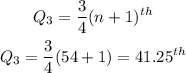
The 3rd quartile is between the 41st and 42nd value

41st value = 413.2

42nd value = 413.2

Take the average of these two values

`Q_3=(413.2+413.2)/(2)=413.2`

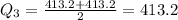
The 3rd quartile is 413.2

The interquartile range (IQR) is the difference between the 3rd and 1st quartiles.

`IQR=Q_3-Q_1=413.2-343.6=69.6`

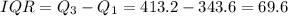
The interquartile range is 69.6