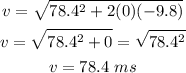Question

A trebuchet fired a tennis ball with an initial velocity. Determine the following

Answer 1

`\begin{gathered} (a)\text{ }12.61\text{ }s \\ (b)\text{ }194.73m \\ (c)\text{ }608.57\text{ }m \\ (d)\text{ }78.4\text{ }m\/s \end{gathered}`

Step-by-step explanation

Parameters given:

Initial velocity, v0 = 78.4

Angle of projectile, θ = 52 degrees

(a) To find the flight time of the tennis ball, apply the formula:

`t=(2v_0\sin\theta)/(g)`

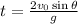
where g = acceleration due to gravity

Hence, the total flight time of the tennis ball is:

`\begin{gathered} t=(2*78.4*\sin52)/(9.8) \\ t=12.61\text{ }s \end{gathered}`

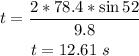
(b) To find the maximum altitude of the ball during its flight, apply the formula:

`H=(v_0^2\sin^2\theta)/(2g)`

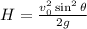
Therefore, the maximum height attained by the tennis ball is:

`\begin{gathered} H=(78.4^2*\sin^2(52))/(2*9.8) \\ H=194.73\text{ }m \end{gathered}`

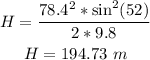
(c) To find the horizontal distance the tennis ball travels, apply the formula:

`R=(v_0^2\sin2\theta)/(g)`

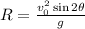
Hence, the horizontal distance traveled by the tennis ball is:

`\begin{gathered} R=(78.4^2*\sin(2*52))/(9.8) \\ R=608.57\text{ }m \end{gathered}`

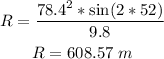
(d) To find the final velocity of the tennis ball, apply the formula:

`v=√(v_0^2+2h(-g))`

where h = initial height = 0 m

Hence, the final velocity of the tennis ball just before impact is:

`\begin{gathered} v=√(78.4^2+2(0)(-9.8)) \\ v=√(78.4^2+0)=√(78.4^2) \\ v=78.4\text{ }m\/s \end{gathered}`