ANSWER
The solutions are:
• x = 0
,
• x = -6
,
• x = -8
EXPLANATION
First we can see that there's and x in every term of the polynomial, so one of the solutions to the equation is when x = 0, because x is a common factor:
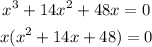
The other two solutions - we know that there are three because the degree of the polynomial is 3 - are the zeros of the polynomial in parenthesis. We can solve it with the formula:
![\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uuterq6bz1kwr2mb9jy58c523r5v4v644y.png)
In our polynomial, a = 1, b = 14 and c = 48:
![\begin{gathered} x=\frac{-14\pm\sqrt[]{14^2-4\cdot48}}{2} \\ x=\frac{-14\pm\sqrt[]{196-192}}{2} \\ x=\frac{-14\pm\sqrt[]{4}}{2} \\ x=(-14\pm2)/(2) \\ x_1=(-14-2)/(2)=(-16)/(2)=-8 \\ x_2=(-14+2)/(2)=(-12)/(2)=-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6mq9suqzj2nh15c248wjmt7jfvasbmi57p.png)
Therefore the solutions to the equation are x = 0, x = -8 and x = -6