Question

A ball collides with a second ball at rest. As a result of the collision, the first ball comes to rest and the second ball moves off at the speed of the first ball. In this collision

Answer 1

Given that the velocities of the two balls are interchanged after the collision.

In an elastic collision, the velocities of the two balls after the collision is given by,

`\begin{gathered} v_1=(m_1-m_2)/(m_1+m_2)u_1+(2m_2)/(m_1+m_2)u_2 \\ v_2=(2m_1)/(m_1+m_2)u_1+(m_2-m_1)/(m_1+m_2)u_2 \end{gathered}`

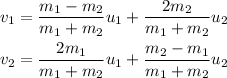
Where m₁ and m₂ are the masses of the two balls and u₁ and u₂ are the velocities of the balls before the collision.

If the masses of the objects are the same and equal to m, then from the above equation,

`\begin{gathered} v_1=\frac{m-m_{}}{m_{}+m_{}}u_1+\frac{2m_{}}{m_{}+m_{}}u_2 \\ =0+u_2 \\ =u_2 \end{gathered}`

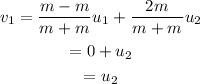
And,

`\begin{gathered} v_2=\frac{2m_{}}{m_{}+m}u_1+\frac{m_{}-m}{m_{}+m}u_2_{} \\ =u_1 \end{gathered}`

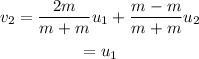
From the above two results, it is clear that in an elastic collision between two balls of equal masses, the velocities of the objects are interchanged after the collision.

Thus, the given collision is the elastic collision between two balls of equal masses.

Therefore, in this collision the masses are equal and the total kinetic energy is conserved.