Question

Answer the questions below about the quadratic function. g(x) = 3x ^ 2 - 6x + 5

Answer 1

In order to find a critical value (maximum or minimum) we need to compute the first derivative, which is given by

`(d)/(dx)g(x)=6x-6`

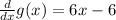
Then, a critical value ocurrs when

`(d)/(dx)g(x)=0`

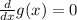
which implies that

`6x-6=0`

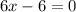
So by adding 6 to both side, we have

`\begin{gathered} 6x=6 \\ then \\ x=(6)/(6) \\ x=1 \end{gathered}`

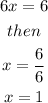
Therefore, there is a maximum or minimum at x=1.

In order to see if the point represents a maximum or minimum, we need to find the second derivative of our function, which is given by

`(d^2)/(dx^2)g(x)=6`

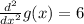
We have that if the second derivative is positive, the point represents a minimum and if it is negative, the point represents a maximum. In our case, since the second derivative is greater than zero (positive number) there is a minimum point at x=1. Then, by substituting this values into the function, we get

`\begin{gathered} g(1)=3(1^2)-6(1)+5 \\ g(1)=3-6+5 \\ g(1)=2 \end{gathered}`

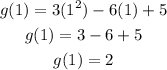
so the minimum point is located at (1,2).

Therefore, with the above information, the answers are:

Does the function have a minimum or maximum values? Answer: Minimum

Where does the minimum or maximum value occur? Answer: x=1

Whats is the funtion's minimum or maximum values? Answer: 2