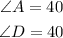Answer:
A = 40
D = 40
Explanation
The triangle ABE and DEF congruent, meaning they have the same measures of sides and angles.
This means angles A and D are equal; therefore,
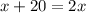
subtracting x from both sides gives
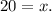
With the value of x in hand, we now find the measures of A and B
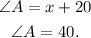
and
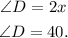
Hence,