ANSWER

Step-by-step explanation
We want to find the equation of the perpendicular bisector of the segment with the endpoints G(3,7) and H(-1,-5).
Since the line is a bisector, it means that it passes through the midpoint of G and H.
Also, since it is perpendicular to the line with endpoints G and H, it means that the slope is the negative inverse of the slope of the line between the two points.
First, find the midpoint of the two points G and H:
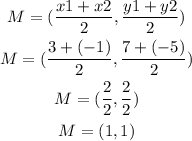
Next, find the slope of the line between points G and H:
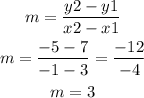
Now, find the negative inverse:

Find the equation of the line using the point-slope method:
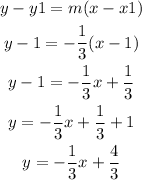
That is the equation of the line.