Question

An ohmic conductor has a resistance R = 100 Ω. It is crossed, for 30 min, by an electric current of intensity I = 0.50 A. a) Calculate the value W¹, of the thermal energy dissipated in this conductor. Give the answer in J and in kWh. b) Deduce the electrical energy consumed by this conductor for the same duration. c) Determine the value of the thermal power dissipated in this conductor. d) What will be the electrical energy W², consumed by this conductor, for a period of 30 min, if the value of the intensity I is doubled? Compare W¹ and W².

Answer 1

Answer:

a) The thermal energy in Joules, W¹ = 45000 Joules

The thermal energy in kWh, W¹ = 0.0125 kWh

b) The electrical energy consumed by this conductor for the same duration = 0.0125 kWh

c) The thermal power = 25 Watts

d) The electrical energy, W² = 180 kJ

Step-by-step explanation:

The resistance of the ohmic conductor, R = 100Ω

The time taken, t = 30 min

t = 30 x 60 seconds

t = 1800 seconds

The current, I = 0.50 A

a) The thermal energy, W¹ dissipated in the conductor is claculated as:

W¹ = I² x R x t

Substitute I = 0.50, t = 1800, R = 100 into the formula above

W¹ = 0.50² x 100 x 1800

W¹ = 45000 Joules

W¹ = 45 kJ

`\begin{gathered} 1\text{ Joule = 2.78}*10^(-7)kWh \\ 45000\text{ Joules = 45000}*2.78*10^(-7) \\ 45000\text{ Joules = }0.0125\text{ kWh} \end{gathered}`

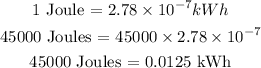
W¹ = 0.0125 kWh

b) The electrical energy consumed by the conductor for the same duration

According to the principle of energy conservation

The electrical energy consumed by the conductor = Thermal energy dissipated in the conductor

Therefore:

The electrical energy consumed by this conductor for the same duration = 0.0125 kWh

c) The value of the thermal power dissipated in this conductor

The thermal power = The thermal energy / Time

The thermal power = 45000/1800

The thermal power = 25 Watts

d) The electrical energy W², consumed by this conductor, for a period of 30 min, if the value of the intensity I is doubled

If the current intensity is doubled, I = 2(0.50)

I = 1 A

The resistance, R = 100 Ω

The time, t = 30 min = 30 x 60 seconds

t = 1800 seconds

W² = I² x R x t

W² = 1² x 100 x 1800

W² = 1 x 100 x 1800

W² = 180000 Joules

The electrical energy if the value of the intensity is doubled, W² = 180 kJ