Given:
The points W and X on the line WX are :
W(-2, 4), X(1, 1)
The points Y and Z on the line YZ are:
Y(1, 2), Z(5, -2)
We can check if the lines are parallel, perpendicular or neither by finding the slope/gradient of each line.

The slope of any line can be found using the formula:
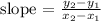
The slope of line WX:
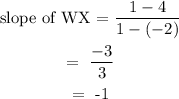
The slope of line YZ:
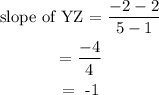
Since the slope of line WX is equal to the slope of line YZ, the lines are parallel.