ANSWER
A. Two complex roots
Step-by-step explanation
We want to describe the roots of the equation:
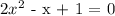
Let us solve it with the quadratic formula.
For a quadratic equation:
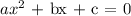
The roots are gotten by using the formula:
![x\text{ = }\frac{-b\text{ }\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/high-school/m0j8pu24gfymkns6fu51zfx9p2t3dh87jg.png)
So, we have that:
a = 2, b = -1, c = 1
So:
![\begin{gathered} x\text{ = }\frac{-(-1)\text{ }\pm\sqrt[]{(-1)^2\text{ - 4(2)(1)}}}{2\cdot2}=\frac{1\text{ }\pm\sqrt[]{1\text{ - 8}}}{4} \\ x\text{ = }\frac{1\text{ }\pm\sqrt[]{-7}}{4}\text{ = }\frac{1\text{ }\pm\text{ }\sqrt[]{7}\cdot\text{ }\sqrt[]{-1}}{4} \\ \Rightarrow\text{ x = }\frac{1\text{ + }\sqrt[]{7}i}{4}\text{ and }\frac{1\text{ - }\sqrt[]{7}i}{4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7adee0wel2txelz1wmxhwbp2ugapkhokwa.png)
As we can see, the two roots of the equation are complex.