Question

F(x) = = between x=4 and x = 7 using the "midpoint rule" with two rectangles of equal width.

Answer 1

Step-by-step explanation

Since we have the function f(x)= 1/x

`\int _a^bf\left(x\right)dx\:\approx \Delta \:x\left(f\left((x_0+x_1)/(2)\right)+f\left((x_1+x_2)/(2)\right)+f\left((x_2+x_3)/(2)\right)+...+f\left((x_(n-1)+x_n)/(2)\right)\right)`
`\mathrm{where}\:\Delta \:x\:=\:(b-a)/(n)`

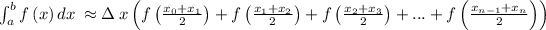
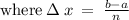
Given a=4, b=7, n=2

`Δx=(7-4)/(2)=(3)/(2)`

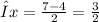
Divide the interval, 4<=x<=7 into 2 subintervals:

`x_0=4,\:x_1=(11)/(2),\:x_2=7`
`=(3)/(2)\left(f\left((x_0+x_1)/(2)\right)+f\left((x_1+x_2)/(2)\right)\right)`

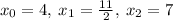
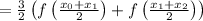
Calculate the subintervals:

`f\left((x_0+x_1)/(2)\right)=f\left((4+(11)/(2))/(2)\right)`
`=f\left((19)/(4)\right)`
`=(1)/((19)/(4))`
`=(4)/(19)`
`f\left((x_1+x_2)/(2)\right)=f\left(((11)/(2)+7)/(2)\right)`
`=(4)/(25)`
`=(3)/(2)\left((4)/(19)+(4)/(25)\right)`

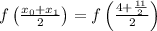
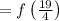
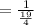
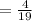
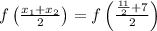
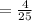
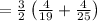
Applying the distributive property and adding fractions:

`=(264)/(475)`

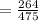
In conclusion, the solution is 264/475