GIVEN:
You roll a fair six-sided die.
You win $10 if you roll at least 4
You lose $3 if you roll the numnber 3.
If you roll any other number, you will neither win nor lose.
Required;
Find the expected value of this probability experiment.
Step-by-step solution;
We shall take the expected winning or loss from each condition given;
![\begin{gathered} Probability\text{ }of\text{ }at\text{ }least\text{ }5: \\ \\ P[rolling\text{ }a\text{ }5]=(1)/(6) \\ \\ P[rolling\text{ }a\text{ }6]=(1)/(6) \\ \\ P[rolling\text{ }a\text{ }5\text{ }or\text{ }6]=(1)/(6)+(1)/(6) \\ \\ =(1)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mpsmsot4ydizr5pfp842i2uyyouxz3a7tp.png)
For this outcome, we now have;
![\begin{gathered} Expected\text{ }value=P[at\text{ }least\text{ }5]*10 \\ \\ EV=(1)/(3)*10 \\ \\ EV=3.33 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kwdbutyuhqfji72pmzncfs9tx4n6fd1to0.png)
The probability of rolling a 3 is;
![P[rolling\text{ }a\text{ }3]=(1)/(6)](https://img.qammunity.org/2023/formulas/mathematics/college/lz86nnu4mxve2km6fq0gk2q0strtv50m9j.png)
Therefore, the expected value is now;
![\begin{gathered} EV=P[rolling\text{ }a\text{ }3]*(-3) \\ \\ EV=(1)/(6)*(-3) \\ \\ EV=-0.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ltw84rums0svtcxckxye6nvgknc7816x0g.png)
If you roll any other number you will neither win nor lose.
Therefore the expected value for rolling any other number will be zero (that is, the probability multiplied by $0).
Therefore, the expected value (winnings) of this probability experiment would be;
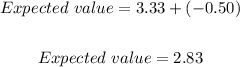
ANSWER:
The expected value of playing this game with the conditions given is $2.83