Question

An astronaut weighing 202 lbs on Earth is on a mission to the Moon and Mars.(a) What would he weigh in newtons when he is on the Moon? The acceleration due to gravity on the Moon is one-sixth thaton Earth. Answer inN(b) How much would he weigh in newtons when he is on Mars, where the acceleration due to gravity is 0.38 times that onEarth? Answer in N(c) What is his mass on Earth? Answer in kg(d) Which of the following are true? (Select all that apply.)His mass on the Moon is smaller than his mass on Earth.His mass on Mars is greater than his mass on Earth.His mass on the Moon is exactly equal to his mass on Earth.His mass on Mars is exactly equal to his mass on Earth.His mass on the Moon is greater than his mass on Earth.His mass on Mars is smaller than his mass on Earth.

Answer 1

(a) 149.8 N

(b) 341.6 N

(c) 91.72 kg

(d)

3rd option: His mass of her on the Moon is exactly equal to his mass of her on Earth.

4th option: His mass of him on Mars is exactly equal to his mass of him on Earth.

Explanation:

Astronaut weight (W) = 202 lbs

We convert it to newtons knowing that 1 lbs is 4.45 N, like this:

`W=202\text{ lbs}\cdot\frac{4.45\text{ N}}{1\text{ lbs}}=898.9\text{ N}`

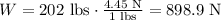
(a)

The weight on the moon will be:

`\begin{gathered} W_m=(1)/(6)\cdot W \\ \\ \text{ We replacing:} \\ \\ W_m=(1)/(6)\cdot898.9 \\ \\ W_m=149.8\text{ N} \end{gathered}`

(b)

To determine the weight on Mars, we must first calculate the mass of the astronaut, like this:

`\begin{gathered} W=m\cdot g \\ \\ \text{ We replacing:} \\ \\ 898.9=m\cdot9.8 \\ \\ m=(898.9)/(9.8)=91.72\text{ kg} \end{gathered}`

Now, we calculate the weight, knowing that the gravity on Mars is 0.38 times that on Earth, like this:

`\begin{gathered} W_M=m\cdot g_M\rightarrow W_M=^m\cdot0.38\cdot g \\ \\ \text{ we replacing:} \\ \\ W_M=91.72\cdot0.38\cdot9.8 \\ \\ W_M=341.6\text{ N} \end{gathered}`

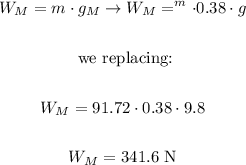
(c)

The mass of the astronaut was calculated in the previous section, where it is equal to 91.72 kg

(d)

The mass remains constant wherever the astronaut is, it does not depend on gravity.

Therefore, the correct options are:

3rd option: His mass of her on the Moon is exactly equal to his mass of her on Earth.

4th option: His mass of him on Mars is exactly equal to his mass of him on Earth.