a)
The composite function f of g is defined as:
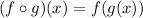
This means that we need to plug function g(x) instead of x in the expression for f(x). Then we have:
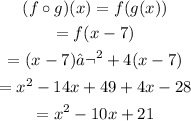
Therefore:

b)
In this case we are looking for the function:
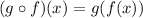
Which means that we need to plug f(x) instead of x in the expression for g(x). With this in mind we have:
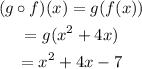
Therefore:

c)
Following similar steps as the previous questions we have:
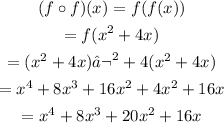
Therefore:

d)
In this case we have:
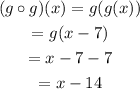
Therefore:
