Question

Determine the value of x that would make lines a and b parallel. X=

Answer 1

If the two lines are parallel, the indicated angles formed by the transversal are Exterior Alternate Angles. Thus, they are equal to each other.

Hence, we can calculate the variable as

`3y+53=7y-55`

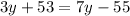
Solving by collecting like terms, we have

`\begin{gathered} 3y-7y=-55-53 \\ -4y=-108 \end{gathered}`

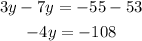
Dividing both sides by -4, we have

`\begin{gathered} y=(-108)/(-4) \\ y=27 \end{gathered}`

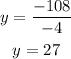
Hence, the value of y is 27.