We have a line that passes through (3, 7) and has a slope of 3/4.
We can find the equation by writing it in slope-point form and then rearrange it:
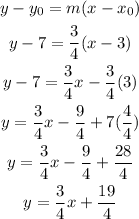
The equation of the line is y = 3/4*x + 19/4.
If point A = (x,5) belongs to the line, we can find x as:
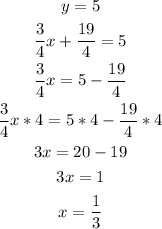
Answer:
The equation of the lineis y = 3/4*x + 19/4.
If point A(x,5) lies on the line, the value of x is 1/3.