Question

Which equation is the inverse of the function+f(x) = -7x-4-3A) F'(x) = -1 -2B) '(x)=-*-4172) $'(x) = -x – 2D) f'(x)=-1 - **534.

Answer 1

To answer this question, the first step we need to do is solve the equation for x. Then, we have:

`y=-7x-4\Rightarrow y+4=-7x\Rightarrow x=((y+4))/(-7)\Rightarrow y=-((y+4))/(7)=(-y-4)/(7)`

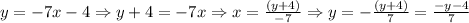
Then, changing y by x, we finally have that the inverse function is:

`f^(-1)(x)=(-x-4)/(7)`

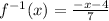
To check this result, if we have that x = 1 for the first equation, the value of y is:

`y=-7(1)-4=-7-4=-11`

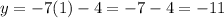
If we use this result in the inverse function, then we must have y = 1 ( that is the original value). That is

`f^(-1)(-11)=\text{ }(-(-11)-4)/(7)=(11-4)/(7)=(7)/(7)=1`

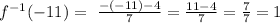
Therefore, option 3 is the answer.