Given,
The Mach number of the aircraft on the earth, M₁=20
The temperature at which the Mach number was measured, T=5 °C
The speed of sound in hydrogen, v=1267 m/s
The speed of the sound at 5 °C is u=334.4 m/s
The Mach number of the aircraft on the earth is given by,
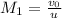
Where v₀ is the speed of the aircraft.
On substituting the known values,
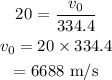
The Mach number of the other world is given by,

On substituting the known values,
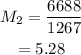
Thus the Mach number on the other world is 5.28