Question

I need answers to this problem !!A swimming pool and house are on a rectangular piece of land. The length of the land is (x + 3) and the width of the land is (x - 9) feet.

Answer 1

ANSWERS

a.

b. 32 sections of fencing

c. He will not have enough to fence the land

Step-by-step explanation

a. It is said in the statement of this problem that the piece of land is rectangular, so the polynomial to represent the piece of land is a rectangle with dimensions (x + 3) and (x - 9).

b. In this part of the problem, we have to assume that x = 50, so the dimensions of the piece of land are,

`\begin{gathered} L=x+3=50+3=53ft \\ W=x-9=50-9=41ft \end{gathered}`

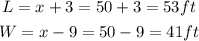
If the homeowner wants to fence the entire piece of land, we have to find the perimeter of the rectangle,

`P=L+L+W+W=2L+2W=2\cdot53ft+2\cdot41ft=106ft+82ft=188ft`

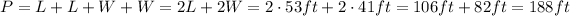
Each piece of fence measures 6 feet. To find how many pieces are needed, we have to divide the total length of the fence - which is the perimeter of the piece of land, by the length of each piece of fencing,

`188ft/6ft=31.3333...`

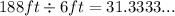
The number of pieces needed must be a whole number. If the homeowner buys 31 pieces, it won't be enough to cover the entire perimeter,

`6ft\cdot31=186ft\text{ }\Rightarrow\text{ }less\text{ }than\text{ }188ft`

Hence, the number of fencing pieces needed is 32.

c. In part b, we found that he needs 32 pieces of fencing. If each costs $47.25, then the total for the entire piece of land would be,

`32\cdot47.25=1512`

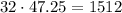
But the homeowner has only $1500 to spend. Hence, since the total fencing costs $1512, he will not have enough to fence the land.