Question

You want to put up a fence that encloses a triangular region with an area greater than or equal to 60 square feet. What is the least possible value of c? Explain.

Answer 1

Hello there. To solve this question, we'll need to remember some properties about triangles.

First, the area of a right triangle as in the following drawing:

Can be calculated by the formula:

`A=(a\cdot b)/(2)`

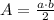
If the area of the enclosed triangular region is greater than or equal to 60, we have the following inequality;

`A\ge60`

Now, using the lengths of the sides of the triangle, we'll have:

`A=(c\cdot12)/(2)=6c`

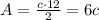
Therefore

`6c\ge60`

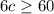
Divide both sides of the inequality by a factor of 6

`c\ge10`

The least possible value of c is 10 ft.