Question

The point B lies on the segment AC.Find the coordinates of B so that the ratio of AB to BC is 1 to 4.A (-22,-25)B (?, ?)C (3,5)

Answer 1

B(-17,-19)

Step-by-step explanation:

The coordinates of a point in a segment that goes from A(x1, y1) to C(x2, y2) in a ratio of a to b can be calculated as

`\begin{gathered} \text{ x-coordinate = }(a)/(a+b)(x_2-x_1)+x_1 \\ \\ \text{ y-coordinate = }(a)/(a+b)(y_2-y_1)+y_1 \end{gathered}`

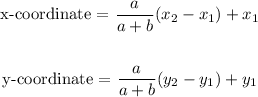
In this case, A(x1, y1) = (-22, -25) and C(x2, y2) = (3, 5) and the ratio is 1 to 4, so a = 1 and b = 4. Replacing the values, we get:

`\begin{gathered} x-coordinate=(1)/(1+4)(3-(-22))-22 \\ \\ x-coordinate=(1)/(5)(3+22)-22=(1)/(5)(25)-22=5-22=-17 \end{gathered}`
`\begin{gathered} y-coordinate=(1)/(1+4)(5-(-25))-25 \\ \\ x-coordinate=(1)/(5)(5+25)-25=(1)/(5)(30)-25=6-25=-19 \end{gathered}`

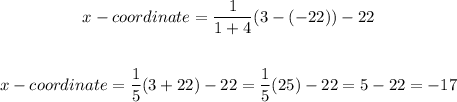
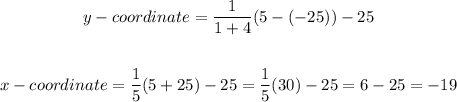
Therefore, the coordinates of B are (x,y) = (-17,-19)