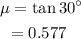Question

Starting from rest, a(n)9 kg block slides 11 mdown a frictionless ramp (inclined at 30◦fromthe floor) to the bottom. The block thenslides an additional 20.8 m along the floorbefore coming to stop.The acceleration of gravity is 9.8 m/sFind the speed of the block at the bottomof the ramp.Answer in units of m/s.018 (part 2 of 3) 10.0 pointsFind the coefficient of kinetic friction betweenblock and floor.019 (part 3 of 3) 10.0 pointsFind the magnitude of the mechanical energylost due to friction.Answer in units of J.

Answer 1

Given that the mass of the block is m = 9 kg.

The length of the ramp is d= 11 m.

The angle is 30 degrees.

Also, the initial speed of the block is u = 0.

The acceleration due to gravity is g =9.8 m/s^2

After moving down the ramp the block moves an additional distance d' = 20.8 m.

We have to find the speed of the block.

The speed can be calculated by the formula

`\begin{gathered} v=\sqrt[]{2gd} \\ =\sqrt[]{2*9.8*11} \\ =14.68\text{ m/s} \end{gathered}`

The coefficient of kinetic friction is

`\begin{gathered} \mu=\tan 30^(\circ) \\ =0.577\text{ } \end{gathered}`