Question

8.4E7 - Num 13.34E8 - Num 2 Find the Quotient (Divide Num 1 by Num2) of these two numbers.Round your answer to 3 significant digits.

Answer 1

We are given the following numbers in scientific notation:

`\begin{gathered} \text{ num1=8.4}*10^7 \\ \text{ num2=3.34}*10^8 \end{gathered}`

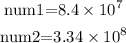
In order to determine the quotient between these two numbers we will first rewrite as a fraction, like this:

`(8.4*10^7)/(3.34*10^8)`

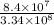
Now we will use the following property of exponent for the powers of ten:

`(x^a)/(x^b)=x^(a-b)`

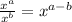
Applying the property we get:

`(8.4)/(3.34)*10^(7-8)`

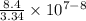
Solving the operation we get:

`(8.4)/(3.34)*10^(-1)`

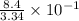
Now we solve the quotient:

`2.51*10^(-1)`

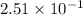
We can further simplify the answer by bringing the 10 to the denominator and changing the sign of its exponent:

`(2.51)/(10)=0.251`

Therefore, the quotient between the two numbers is 0.251.