general geometric formula is
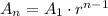
then we replace using A3
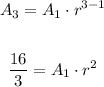
now replace using A5
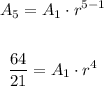
now we have two equations and two unknow
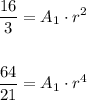
we can solve A1 or r from any equation and replace on the other
I will solve A1 from the first equation
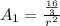
and replace on the second to solve r
![\begin{gathered} (64)/(21)=(((16)/(3))/(r^2))\cdot r^4 \\ \\ (64)/(21)=(16)/(3)\cdot r^2 \\ \\ r^2=(64*3)/(21*16) \\ \\ r^2=(192)/(336)=(4)/(7) \\ \\ r=\frac{2\sqrt[]{7}}{7} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y1btuujcl5odbhlnu236y8m73b790ujuxc.png)
now replace r on the other equation to find A1
![\begin{gathered} (16)/(3)=A_1\cdot(\frac{2\sqrt[]{7}}{7})^2 \\ \\ (16)/(3)=A_1\cdot(4)/(7) \\ \\ A_1=(16*7)/(4*3) \\ \\ A_1=(28)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/emmzl1s5qdccgnheuc01s3aqjf7v70jpji.png)
now we have the two unknows A1 and r then replace on the general geometric equation
![A_n=(28)/(3)\cdot(\frac{2\sqrt[]{7}}{7})^(n-1)](https://img.qammunity.org/2023/formulas/mathematics/college/518wz1ntm52l6vzyd081davc6alglhoh0p.png)