Answer
The height of the plane at that time is 1.1 miles
The distance of the plane's path is 10.1 miles
Step-by-step explanation
The situation models a right angle triangle as shown below
Using trigonometric ratio,
tan 6° = opposite / adjacent
The opposite side of the triangle is the height of the plane. The distance traveled horizontally is the adjacent side. Therefore,
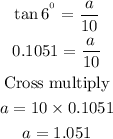
The height of the plane at that time ≈ 1.1 miles
The hypotenuse of the triangle formed is the distance of the plane path.
Therefore, this distance can be calculated using Pythagoras rule as follows:
![\begin{gathered} c^2=a^2+b^2 \\ a=1.051\text{ miles} \\ b=10\text{ miles} \\ \Rightarrow c^2=1.051^2+10^2 \\ c^2=1.104601+100 \\ c^2=101.104601 \\ c=\sqrt[]{101.104601} \\ c=10.05507837\text{ miles} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/atekc5azmbqszuyyazgabzxuinlguicvif.png)
The distance of the plane's path = 10.1 miles