Question

I need help and ty.In each problem, first write the equation for the perimeter of the triangle. Then solve the equation and use your solution to find the lengths of all sides.

Answer 1

Given:

Each side of the triangle is given as x-2.

Perimeter of the triangle is, P=294.

The objective is to find the equation of the perimeter and length of sides of the triangle.

It is known that the perimeter of a triangle is addition of all three sides of the triangle.

`\begin{gathered} \text{P}=(x-2)+(x-2)+(x-2) \\ P=3x-6 \end{gathered}`

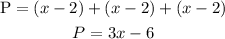
Let's find the sides of the triangle, by substituting the value of perimeter as, P =294.

`\begin{gathered} 294=3x-6 \\ 3x=294+6 \\ 3x=300 \\ x=(300)/(3) \\ x=100 \end{gathered}`

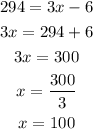
Substitute x in the value of the given side of the triangle.

`\begin{gathered} =x-2 \\ =100-2 \\ =98 \end{gathered}`

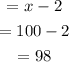
Hence, the equtaion of perimeter of the triangle is 3x-6 and each sides of the triangle is 98.